Particle Image Velocimetry
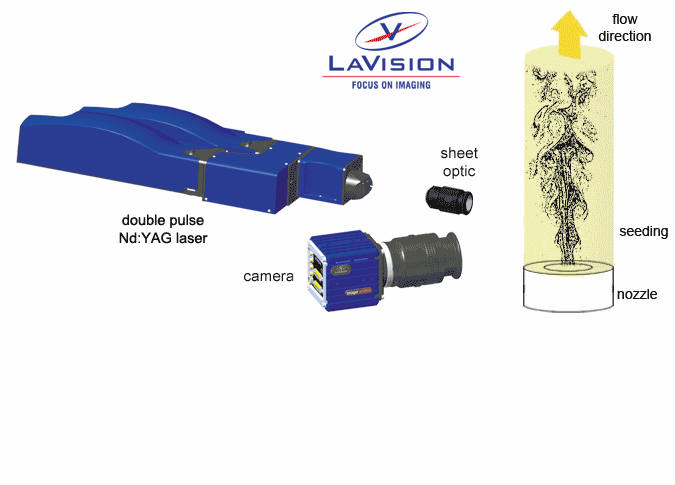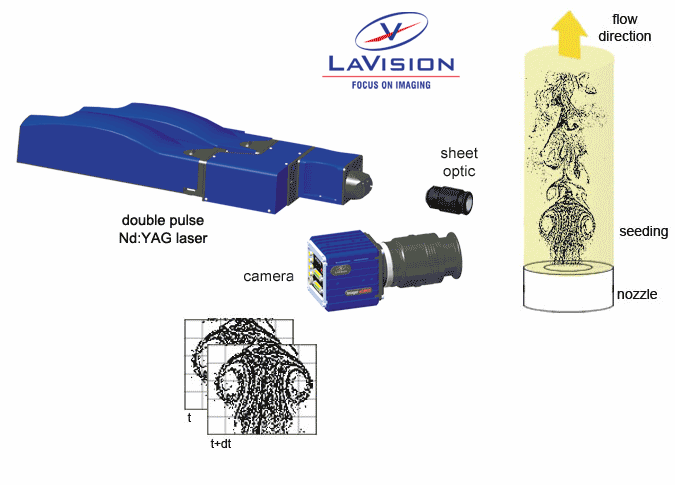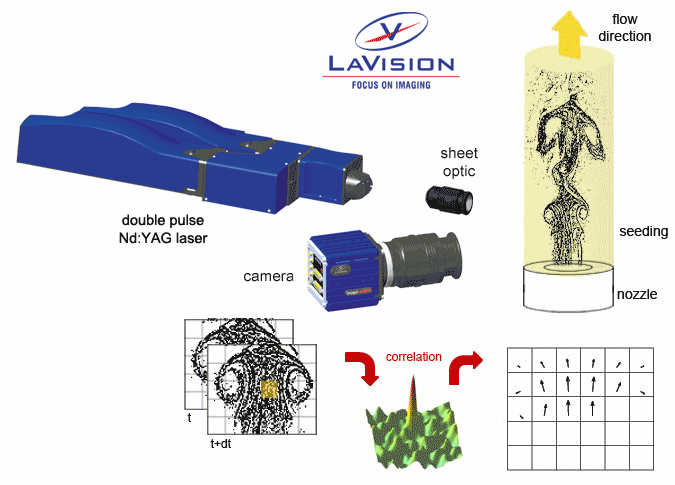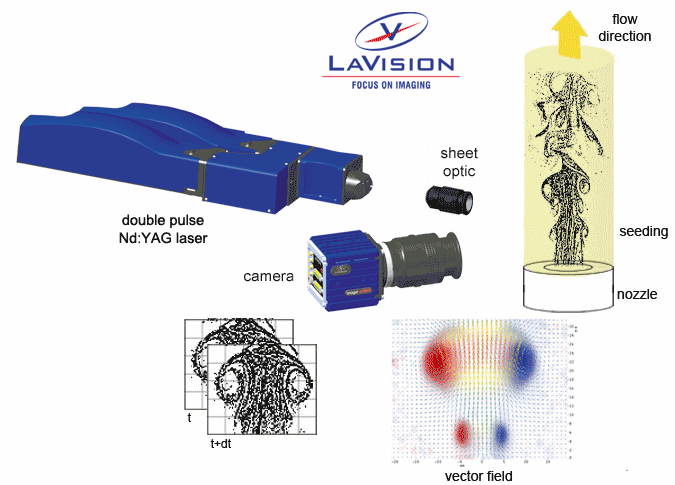
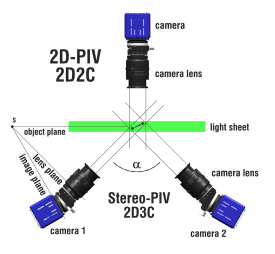
In Particle Image Velocimetry (PIV) light scattering particles are added to the flow. A laser beam is formed into a light sheet illuminating seeding particles twice with a short time interval %delta%t. In 2D-PIV the scattered light is recorded onto two consecutive frames of a high resolution digital camera. In Stereo-PIV two cameras at different observation angles are used to measure also the third (out-of-plane) component of the flow velocity in the light sheet.
For velocity calculation the particle image of each camera is subdivided into small interrogation windows. The average particle displacement within an interrogation window is determined by cross-correlation followed by the localization of the correlation peak. From the known time difference %delta%t and the measured displacement in each direction the velocity components are calculated. Perspective correction, distortion compensation and image mapping of the two views are taken care of by Self-Calibration procedures. Advanced multi-pass image deformation techniques are used for higher accuracy and spatial resolution.

Spatial and temporal derivatives
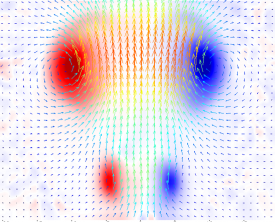
From one velocity field a range of spatial derivatives can be calculated such as vorticity and shear stress. Ensemble statistics provide additional information like turbulent kinetic energy or Reynolds stresses. Timeresolved velocity fields recorded with high-frame-rate cameras and high frequency lasers allow for deeper dynamic insights about flow field evolution, fluid element trajectories, acceleration and turbulence statistics.
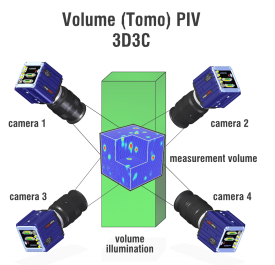
A Tomographic PIV system with typically 2-4 cameras extends the flow measurement into a full volume. Processing is done by tomographic reconstruction of voxel intensities for each time step followed by crosscorrelation between interrogation volumes. This allows for instantaneous measurement of all three velocity components in a three-dimensional measurement volume (3D3C) visualizing the 3D flow structure. The complete velocity gradient tensor can be calculated yielding quantities such as 3D vorticity and strain tensor.
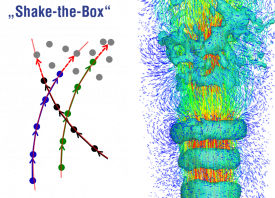
Time-Resolved Particle Tracking Velocimetry
Shake-the-Box (STB) is the most advanced 3D Lagrangian Particle Tracking Velocimetry (PTV) method for densely seeded flows at highest spatial resolution.STB takes advantage of time-resolved particle image sequences to produce accurate Lagrangian particle tracks. The method makes use of the particle based Iterative Particle Reconstruction technique (IPR) to initialize particle tracks over a few recordings (typically four). The positions of tracked particles at following time instants are extrapolated from the initialized tracks; the predicted particle location is then corrected by means of the IPR image matching technique, referred to as shaking.

